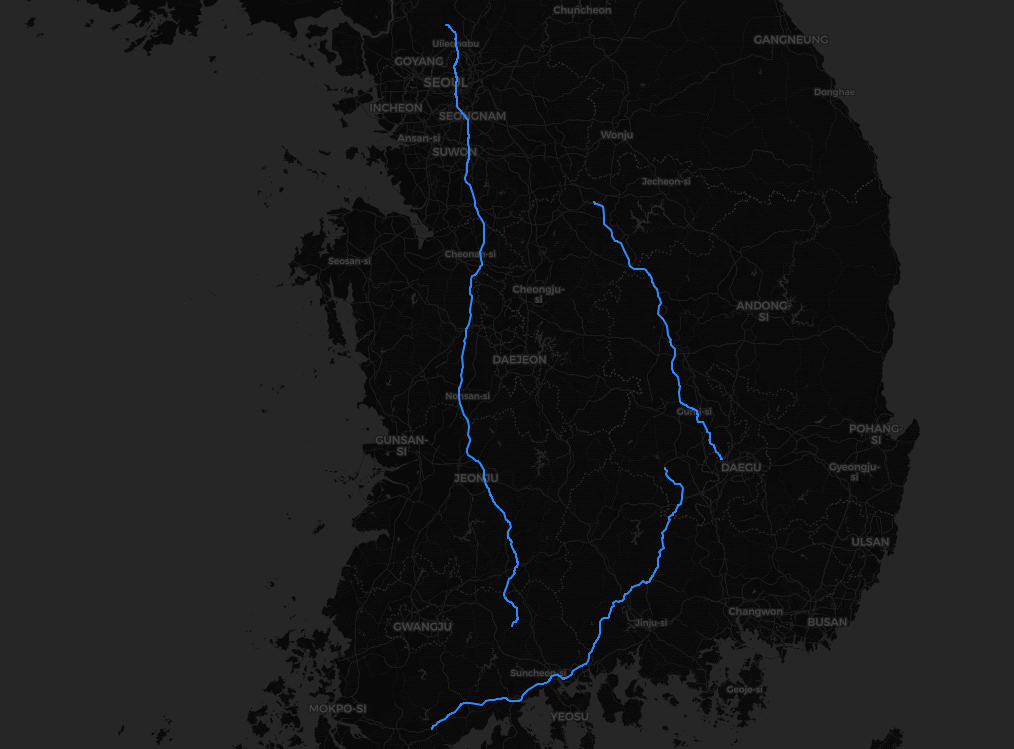
최적 경로 산출

pgrouting에 의한 최적경로 산출

최적경로 산출결과

 

결과 데이터

 

데이터의 출처는...

 

https://www.its.go.kr/nodelink/intro

ITS 국가교통정보센터

 

직스트라(Dijkstra) 방식의 최적거리 산출. 사전에 pgrouting이 설치되어 있어야 한다.

pgrouting은 create extension pgrouting 명령으로 설치한다.

직스트라 알고리즘은 위키피디아에 따르면 다음과 같다. 영어의 압박!!!

 

Let the node at which we are starting be called the initial node. Let the distance of node Y be the distance from the initial node to Y. Dijkstra's algorithm will initially start with infinite distances and will try to improve them step by step.

1. Mark all nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
2. Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes. During the run of the algorithm, the tentative distance of a node v is the length of the shortest path discovered so far between the node v and the starting node. Since initially no path is known to any other vertex than the source itself (which is a path of length zero), all other tentative distances are initially set to infinity. Set the initial node as current.
3. For the current node, consider all of its unvisited neighbors and calculate their tentative distances through the current node. Compare the newly calculated tentative distance to the one currently assigned to the neighbor and assign it the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B through A will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, the current value will be kept.
4. When we are done considering all of the unvisited neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again (this is valid and optimal in connection with the behavior in step 6.: that the next nodes to visit will always be in the order of 'smallest distance from initial node first' so any visits after would have a greater distance).
5. If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
6. Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new current node, and go back to step 3.

When planning a route, it is actually not necessary to wait until the destination node is "visited" as above: the algorithm can stop once the destination node has the smallest tentative distance among all "unvisited" nodes (and thus could be selected as the next "current").

맨 위에 나오는 결과물은 아래의 쿼리로 동작한다. CTE를 써서 중복을 없애야 할텐데 귀차니즘 땜시... 

요즘은 일도 먹는것도 모두 귀찮여.

SELECT seq, node, edge, cost, b.geom FROM pgr_dijkstra(     'SELECT id, f_node as source, t_node target, length cost from link2',     3680002100,      3350064201,      FALSE  ) AS a join moct_link b on a.edge=b.link_id::bigint union all SELECT seq, node, edge, cost, b.geom FROM pgr_dijkstra(     'SELECT id, f_node as source, t_node target, length cost from link2',     2350293201,      3300150901,      FALSE  ) AS a join moct_link b on a.edge=b.link_id::bigint union all SELECT seq, node, edge, cost, b.geom FROM pgr_dijkstra(     'SELECT id, f_node as source, t_node target, length cost from link2',     3690223601,      2720346401,      FALSE  ) AS a join moct_link b on a.edge=b.link_id::bigint